For those who do not like to use the ibuffer, there is another nice feature in Emacs: Just use Ctrl+Left Mouse and you will see a buffer menu appearing which shows all the buffer modes that are active. If you click on one of them all buffers opened are shown (in the image you see the R-files opened at the moment:
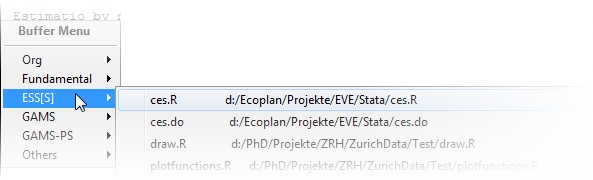
Another nice key shortcut is Ctrl + Right mouse. Depending on the mode you are in it opens a menu with all the commands you can use in that mode (the next image shows you the commands that appear
… Read the rest “More options for working with several buffers” 